Boolean Matematiği Nedir?
Boolean matematiği, yalnızca iki değeri (genellikle "doğru" ve "yanlış" olarak ifade edilen) alan bir matematik dalıdır. George Boole tarafından geliştirilen bu matematik türü, mantıksal ifadelerin ve işlemlerin temelini oluşturur. Boolean matematiği genellikle dijital elektronik devrelerin tasarımında ve bilgisayar biliminde kullanılır.
Boolean matematiğinde kullanılan temel işlemler şunlardır:
1. VE (AND) İşlemi: İki veya daha fazla koşulun aynı anda doğru olup olmadığını kontrol eder. Sonuç yalnızca tüm koşullar doğruysa doğru, en az biri yanlışsa yanlış olur.
Örnek: A VE B (A AND B) ifadesi, A ve B her ikisi de doğruysa doğru sonuç verir.
2. VEYA (OR) İşlemi: İki veya daha fazla koşulun en az birinin doğru olup olmadığını kontrol eder. Sonuç en az bir koşul doğruysa doğru, tüm koşullar yanlışsa yanlış olur.
Örnek: A VEYA B (A OR B) ifadesi, A veya B veya her ikisi doğruysa doğru sonuç verir.
3. DEĞİL (NOT) İşlemi: Bir koşulun tersini alır. Yani, doğruysa yanlış, yanlışsa doğru sonuç verir.
Örnek: DEĞİL A (NOT A) ifadesi, A doğruysa yanlış, A yanlışsa doğru sonuç verir.
Boolean matematiği, bu temel işlemleri kullanarak daha karmaşık mantıksal ifadeler oluşturabilir ve bu ifadeleri analiz edebilir. Bu matematik dalı, bilgisayar programlaması, elektrik mühendisliği, lojistik, mantıksal düşünme ve daha birçok alanda kullanılır.
Dijital Elektronikte Boolean Matematiğinin Kullanımı
Boolean matematiği, dijital elektronikte temel bir rol oynar. Elektronik devrelerin tasarımı ve işleyişi, mantıksal ifadelerin kullanılmasıyla açıklanabilir. İşte Boolean matematiğinin dijital elektronikteki kullanımına dair bazı temel konular:
Mantıksal Kapılar ve Devre Tasarımı
Dijital elektronikte, mantıksal kapılar (AND, OR, NOT vb.) mantıksal sinyalleri işlemek için kullanılır. Boolean matematiği, bu kapıların işlevlerinin anlaşılmasına ve devre tasarımına rehberlik eder. Örneğin, AND kapısı iki giriş sinyalinin mantıksal "ve" işlemini gerçekleştirirken, OR kapısı "veya" işlemini yapar.
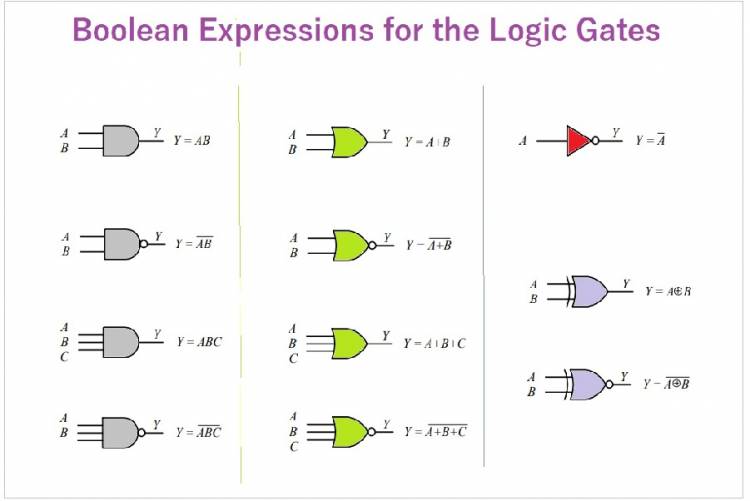
Aşağıda iki girişli (A,B) mantıksal kapıların Baoolean işlemlerinde nasıl kullanıldığına ilişkin bir tablo var:

Boolean matematiği, bilgisayarların temelini oluşturan sayı sistemlerinin ve kodlamalarının anlaşılmasında önemlidir. Örneğin, ikili (binary) sayı sistemi, yalnızca sıfır ve bir kullanarak sayıları temsil eder. Bu sayılar ve semboller, Boolean mantığıyla işlenir.
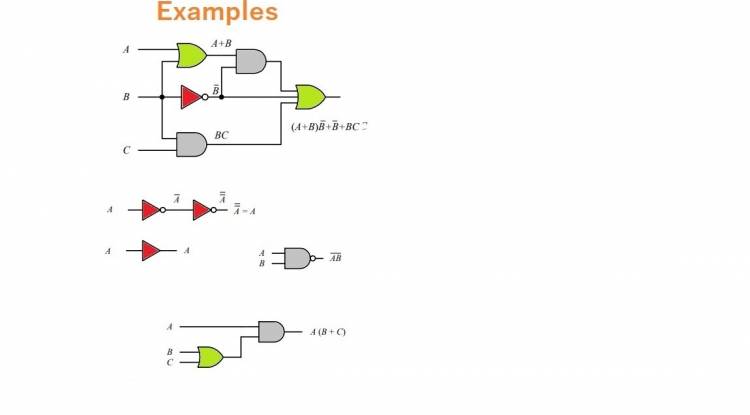
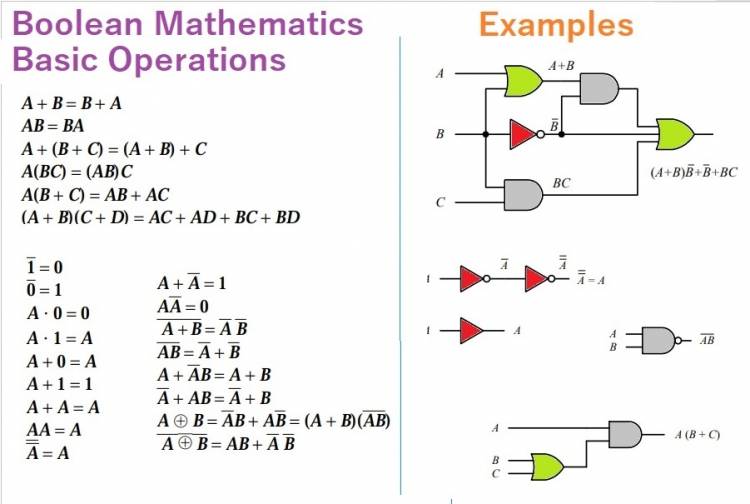
Dijital elektronikte, mantıksal işlemler ve karar mekanizmaları, Boolean matematiğinin temelini oluşturur. Bilgisayar programlamasında kullanılan "if-else" ifadeleri ve mantıksal koşullar, Boolean matematiği sayesinde oluşturulur ve yürütülür. Aşağıda AND, OR, Not mantıksal kapıları ile ilgili örnekler incelenebilir :