What is Boolean Mathematics?
Boolean mathematics is a branch of mathematics that takes only two values (often expressed as "true" and "false"). Developed by George Boole, this type of mathematics forms the basis of logical expressions and operations. Boolean mathematics is often used in the design of digital electronic circuits and in computer science.
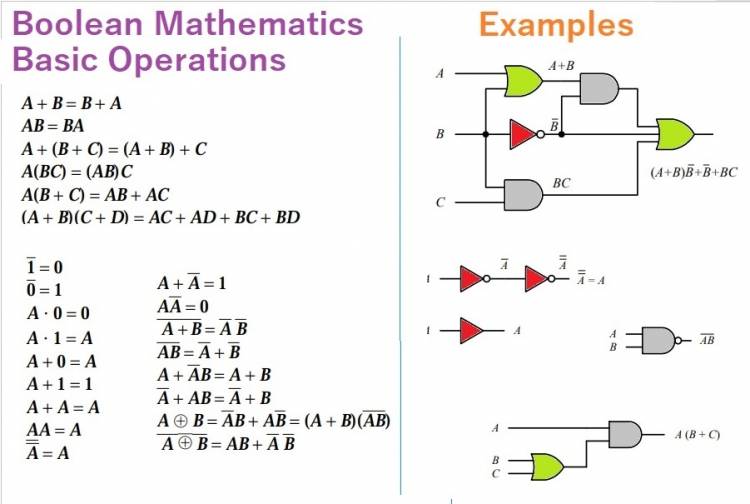
The basic operations used in Boolean mathematics are:
1. AND Operation: Checks if two or more conditions are true at the same time. The result is true only if all conditions are true, and false if at least one of them is false.
Example: The expression A AND B (A AND B) returns true if both A and B are true.
2. OR (OR) Operation: Checks if at least one of two or more conditions is true. The result is true if at least one condition is true, and false if all conditions are false.
Example: A OR B (A OR B) returns true if A or B or both are true.
3. NOT (NOT) Operation: Inverts a condition. That is, it returns false if true and true if false.
Example: NOT A (NOTE A) returns false if A is true and true if A is false.
Boolean math can use these basic operations to create and analyze more complex logical expressions. This branch of mathematics is used in computer programming, electrical engineering, logistics, logical thinking, and more.
Use of Boolean Mathematics in Digital Electronics
Boolean mathematics plays a fundamental role in digital electronics. The design and operation of electronic circuits can be explained using logical expressions. Here are some key topics on the use of Boolean mathematics in digital electronics:
Logical Gates and Circuit Design
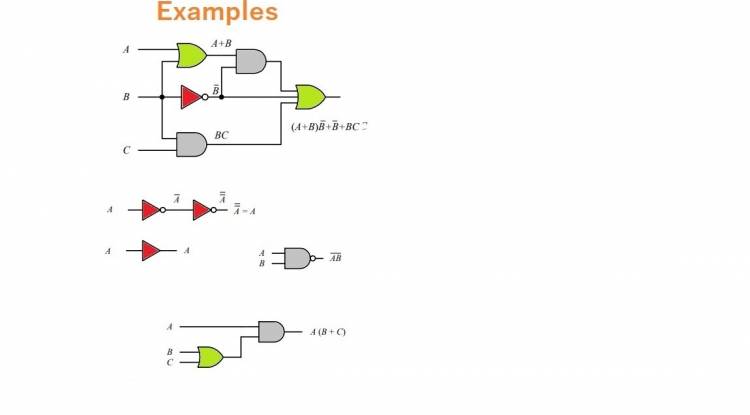
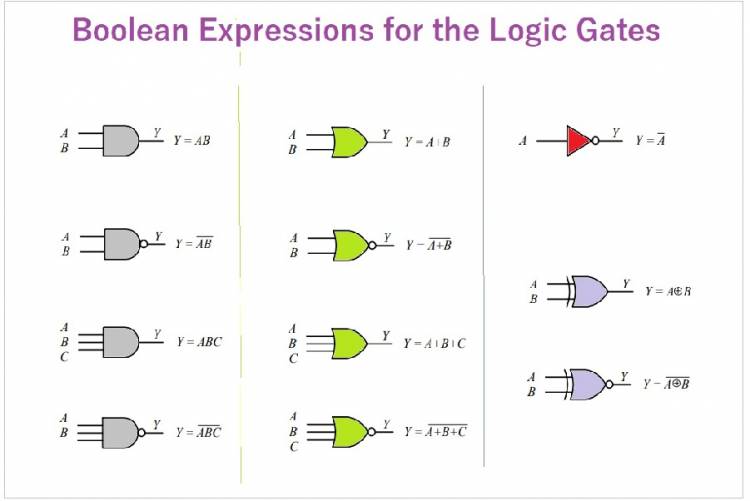
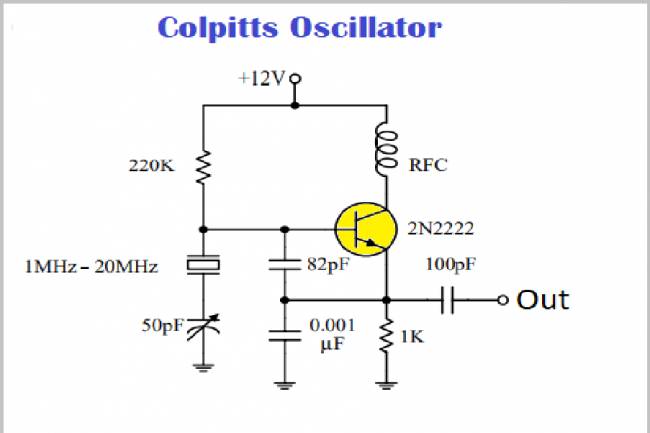
In digital electronics, logic gates (AND, OR, NOT etc.) are used to process logic signals. Boolean mathematics guides the understanding of the functions of these gates and circuit design. For example, the AND gate performs the logical "and" operation of the two input signals, while the OR gate performs the "or" operation.
Below is a table of how two-input (A,B,C) logical gates are used in Baoolean operations:

Boolean mathematics is important in understanding the number systems and encodings that underpin computers. For example, the binary number system represents numbers using only zero and one. These numbers and symbols are handled with Boolean logic.
In digital electronics, logical operations and decision mechanisms form the basis of Boolean mathematics. The "if-else" statements and logical conditions used in computer programming are created and executed by Boolean mathematics. Examples of AND, OR, Not logic gates can be examined below: